Fenwick Tree or Binary Indexed Tree
Related problem in LeetCode:
- [307.] Range Sum Query - Mutable
- [315.] Count of Smaller Numbers after Self
Youtube Video by Tushar Roy
Complexity Analysis
- Space:
O(n) - Time:
- Search:
O(logn) - Update:
O(logn) - Create:
O(n logn)
- Search:
How to get Parent?
- 2’s complement
- AND “
&” with original number - Add it to original number
update tree:
while (i <= n) {
i += lowbit(i);
// update tree
...
}
where lowbit() is a function which you can extract the lower bit from an integer:
-x = ~x + 1
lowbit(x) = x & (-x)
For example:
x = 5 = 0110
-x = ~x + 1 = 1001 + 1 = 1010
lowbit(x) = 0010
so add it back to original number 0010 + 0110 = 1000 = 8, 8 will be the parent of 5
How to get Next?
- 2’s complement
- AND “
&” with original number - Add it to original number
query tree:
while (i > 0) {
i -= lowbit(i);
// update tree
...
}
Binary Indexed Tree or Fenwick Tree [GeeksforGeeks]
Let us consider the following problem to understand Binary Indexed Tree.
We have an array arr[0 . . . n-1]. We should be able to
- Find the sum of first i elements.
- Change value of a specified element of the array
arr[i] = xwhere0 <= i <= n-1.
A simple solution is to run a loop from 0 to i-1 and calculate sum of elements. To update a value, simply do arr[i] = x. The first operation takes O(n) time and second operation takes O(1) time. Another simple solution is to create another array and store sum from start to i at the i‘th index in this array. Sum of a given range can now be calculated in O(1) time, but update operation takes O(n) time now. This works well if the number of query operations are large and very few updates.
Can we perform both the operations in O(log n) time once given the array?
One Efficient Solution is to use Segment Tree that does both operations in O(Logn) time.
Using Binary Indexed Tree, we can do both tasks in O(Logn)time. The advantages of Binary Indexed Tree over Segment are, requires less space and very easy to implement..
Representation
Binary Indexed Tree is represented as an array. Let the array be BITree[]. Each node of Binary Indexed Tree stores sum of some elements of given array. Size of Binary Indexed Tree is equal to n where n is size of input array. In the below code, we have used size as n+1 for ease of implementation.
Construction
We construct the Binary Indexed Tree by first initializing all values in BITree[] as 0. Then we call update() operation for all indexes to store actual sums, update is discussed below.
Operations
getSum(index)
getSum(index): Returns sum of arr[0..index]
// Returns sum of arr[0..index] using BITree[0..n]. It assumes that
// BITree[] is constructed for given array arr[0..n-1]
1) Initialize sum as 0 and index as index+1.
2) Do following while index is greater than 0.
...a) Add BITree[index] to sum
...b) Go to parent of BITree[index]. Parent can be obtained by removing
the last set bit from index, i.e., index = index - (index & (-index))
3) Return sum.
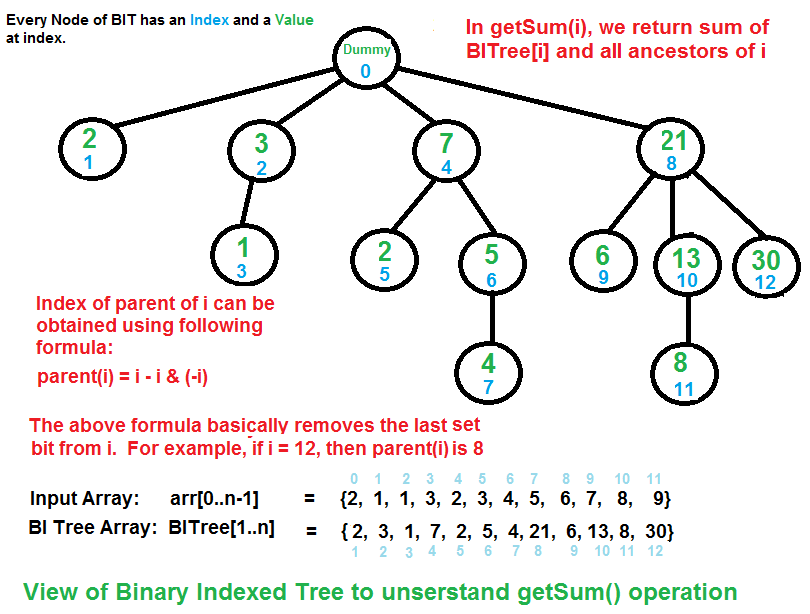
- Node at index
0is a dummy node. - A node at index
yis parent of a node at indexx, iffycan be obtained by removing last set bit from binary representation ofx. - A child
xof a nodeystores sum of elements from ofy(exclusivey) and ofx(inclusivex).
update(index, val)
update(index, val): Updates BIT for operation arr[index] += val
// Note that arr[] is not changed here. It changes
// only BI Tree for the already made change in arr[].
1) Initialize index as index+1.
2) Do following while index is smaller than or equal to n.
...a) Add value to BITree[index]
...b) Go to parent of BITree[index]. Parent can be obtained by removing
the last set bit from index, i.e., index = index + (index & (-index))

The update process needs to make sure that all BITree nodes that have arr[i] as part of the section they cover must be updated. We get all such nodes of BITree by repeatedly adding the decimal number corresponding to the last set bit.
How does Binary Indexed Tree work?
The idea is based on the fact that all positive integers can be represented as sum of powers of 2.
For example 19 can be represented as 16 + 2 + 1. Every node of BI Tree stores sum of n elements where n is a power of 2. For example, in the above first diagram for getSum(), sum of first 12 elements can be obtained by sum of last 4 elements (from 9 to 12) plus sum of 8 elements (from 1 to 8). The number of set bits in binary representation of a number n is O(Logn).
Therefore, we traverse at-most O(Logn) nodes in both getSum() and update() operations. Time complexity of construction is O(nLogn) as it calls update() for all n elements.
Implementation:
Following are the implementations of Binary Indexed Tree.
// Java program to demonstrate lazy
// propagation in segment tree
import java.util.*;
import java.lang.*;
import java.io.*;
class BinaryIndexedTree
{
// Max tree size
final static int MAX = 1000;
static int BITree[] = new int[MAX];
/* n --> No. of elements present in input array.
BITree[0..n] --> Array that represents Binary
Indexed Tree.
arr[0..n-1] --> Input array for whic prefix sum
is evaluated. */
// Returns sum of arr[0..index]. This function
// assumes that the array is preprocessed and
// partial sums of array elements are stored
// in BITree[].
int getSum(int index)
{
int sum = 0; // Iniialize result
// index in BITree[] is 1 more than
// the index in arr[]
index = index + 1;
// Traverse ancestors of BITree[index]
while(index>0)
{
// Add current element of BITree
// to sum
sum += BITree[index];
// Move index to parent node in
// getSum View
index -= index & (-index);
}
return sum;
}
// Updates a node in Binary Index Tree (BITree)
// at given index in BITree. The given value
// 'val' is added to BITree[i] and all of
// its ancestors in tree.
public static void updateBIT(int n, int index,
int val)
{
// index in BITree[] is 1 more than
// the index in arr[]
index = index + 1;
// Traverse all ancestors and add 'val'
while(index <= n)
{
// Add 'val' to current node of BIT Tree
BITree[index] += val;
// Update index to that of parent
// in update View
index += index & (-index);
}
}
/* Function to construct fenwick tree
from given array.*/
void constructBITree(int arr[], int n)
{
// Initialize BITree[] as 0
for(int i=1; i<=n; i++)
BITree[i] = 0;
// Store the actual values in BITree[]
// using update()
for(int i = 0; i < n; i++)
updateBIT(n, i, arr[i]);
}
// Main function
public static void main(String args[])
{
int freq[] = {2, 1, 1, 3, 2, 3,
4, 5, 6, 7, 8, 9};
int n = freq.length;
BinaryIndexedTree tree = new BinaryIndexedTree();
// Build fenwick tree from given array
tree.constructBITree(freq, n);
System.out.println("Sum of elements in arr[0..5]"+
" is = "+ tree.getSum(5));
// Let use test the update operation
freq[3] += 6;
// Update BIT for above change in arr[]
updateBIT(n, 3, 6);
// Find sum after the value is updated
System.out.println("Sum of elements in arr[0..5]"+
" after update is = " + tree.getSum(5));
}
}
// This code is contributed by Ranjan Binwani
Output:
Sum of elements in arr[0..5] is 12
Sum of elements in arr[0..5] after update is 18
Can we extend the Binary Indexed Tree for range Sum in Logn time?
This is simple to answer. The rangeSum(l, r) can be obtained as getSum(r) – getSum(l-1).
Applications:
Used to implement the arithmetic coding algorithm. Development of operations it supports were primarily motivated by use in that case. See this for more details.
Example Problems:
Count inversions in an array | Set 3 (Using BIT)
Two Dimensional Binary Indexed Tree or Fenwick Tree
Counting Triangles in a Rectangular space using BIT
Implementation by HuaHua
class FenwickTree {
public:
FenwickTree(int n): sums_(n + 1, 0) {}
void update(int i, int delta) {
while (i < sums_.size()) {
sums_[i] += delta;
i += lowbit(i);
}
}
int query(int i) const {
int sum = 0;
while (i > 0) {
sum += sums_[i];
i -= lowbit(i);
}
return sum;
}
private:
static inline int lowbit(int x) { return x & (-x); }
vector<int> sums_;
};