Build Neural Network from scratch with Numpy on MNIST Dataset

In this post, I will introduce how to implement a Neural Network from scratch with Numpy and training on MNIST dataset.

Long read and Heavy mathematical notations

This is originally HW1 of CS598: Deep Learning at UIUC.

Build Neural Network from scratch with Numpy on MNIST Dataset

In this post, when we’re done we’ll be able to achieve $ 98\% $ precision on the MNIST dataset. We will use mini-batch Gradient Descent to train and we will use another way to initialize our network’s weights.

Implementation

Prepare MNIST dataset

First, we need prepare out dataset. In this examle, it will be the MNIST dataset. We need One-hot encode the labels of MNIST dataset. If you are not familiar with one-hot encoding, there is another post concerning this topic and can be found here.

# load MNIST data
MNIST_data = h5py.File("../MNISTdata.hdf5", 'r')
x_train = np.float32(MNIST_data['x_train'][:])
y_train = np.int32(np.array(MNIST_data['y_train'][:, 0])).reshape(-1, 1)
x_test  = np.float32(MNIST_data['x_test'][:])
y_test  = np.int32(np.array(MNIST_data['y_test'][:, 0])).reshape(-1, 1)
MNIST_data.close()


# stack together for next step
X = np.vstack((x_train, x_test))
y = np.vstack((y_train, y_test))


# one-hot encoding
digits = 10
examples = y.shape[0]
y = y.reshape(1, examples)
Y_new = np.eye(digits)[y.astype('int32')]
Y_new = Y_new.T.reshape(digits, examples)


# number of training set
m = 60000
m_test = X.shape[0] - m
X_train, X_test = X[:m].T, X[m:].T
Y_train, Y_test = Y_new[:, :m], Y_new[:, m:]


# shuffle training set
shuffle_index = np.random.permutation(m)
X_train, Y_train = X_train[:, shuffle_index], Y_train[:, shuffle_index]

Weight Initialization

After preparing the MNIST dataset, let us dive in the weights initialization in a smarter way!

TL;DR

Calibrating the variances with `1/sqrt(n)`

The outputs from a randomly initialized neuron has a variance that grows with the number of inputs. It turns out that we can normalize the variance of each neuron’s output to $ 1 $ by scaling its weight vector by the square root of its fan-in (i.e. its number of inputs). That is, the recommended heuristic is to initialize each neuron’s weight vector as: w = np.random.randn(n) / sqrt(n), where $ n $ is the number of its inputs. This ensures that all neurons in the network initially have approximately the same output distribution and empirically improves the rate of convergence.

The sketch of the derivation is as follows: Consider the inner product $ s = \sum_i^n w_i x_i $ between the weights $ w $ and input $ x $, which gives the raw activation of a neuron before the non-linearity. We can examine the variance of $ s $:

\[\begin{align} \text{Var}(s) &= \text{Var}(\sum_i^n w_ix_i) \\\\ &= \sum_i^n \text{Var}(w_ix_i) \\\\ &= \sum_i^n [E(w_i)]^2\text{Var}(x_i) + E[(x_i)]^2\text{Var}(w_i) + \text{Var}(x_i)\text{Var}(w_i) \\\\ &= \sum_i^n \text{Var}(x_i)\text{Var}(w_i) \\\\ &= \left( n \text{Var}(w) \right) \text{Var}(x) \end{align}\]

where in the first 2 steps we have used properties of variance. In third step we assumed zero mean inputs and weights, so $ E[x_i] = E[w_i] = 0 $. Note that this is not generally the case: For example ReLU units will have a positive mean. In the last step we assumed that all $ w_i $, $ x_i $ are identically distributed. From this derivation we can see that if we want s to have the same variance as all of its inputs $ x $, then during initialization we should make sure that the variance of every weight $ w $ is $ 1/n $. And since $ \text{Var}(aX) = a^2\text{Var}(X) $ for a random variable $ X $ and a scalar $ a $, this implies that we should draw from unit gaussian and then scale it by $ a = \sqrt{1/n} $, to make its variance $ 1/n $. This gives the initialization w = np.random.randn(n) / sqrt(n).

# initialization
params = {"W1": np.random.randn(opt.n_h, opt.n_x) * np.sqrt(1. / opt.n_x),
          "b1": np.zeros((opt.n_h, 1)) * np.sqrt(1. / opt.n_x),
          "W2": np.random.randn(digits, opt.n_h) * np.sqrt(1. / opt.n_h),
          "b2": np.zeros((digits, 1)) * np.sqrt(1. / opt.n_h)}

Neural Network

Then let’s define our key functions.

Sigmoid

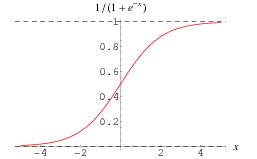
The sigmoid function gives an ‘S’ shaped curve. This curve has a finite limit of:

‘0’ as $ x $ approaches $ - \infty $
‘1’ as $ x $ approaches $ + \infty $

\[y = \frac{1}{1 + \exp(-x)}\]

The output of sigmoid function when $ x=0 $ is $ 0.5 $

Thus, if the output is more than $0.5$ , we can classify the outcome as $1$ (or YES) and if it is less than $0.5$ , we can classify it as $0$ (or NO) .

def sigmoid(z):
    """
    sigmoid activation function.

    inputs: z
    outputs: sigmoid(z)
    """
    s = 1. / (1. + np.exp(-z))
    return s

Loss function

What we use in this example is cross-entropy loss.

\[L(y, \hat{y}) = -y \log(\hat{y}) - (1-y) \log(1-\hat{y}).\]

After averaging over a training set of $ m $ examples, we will have the following:

\[L(Y, \hat{Y}) = -\frac{1}{m} \sum_{i=1}^m \left( y^{(i)} \log(\hat{y}^{(i)}) + (1-y^{(i)}) \log(1-\hat{y}^{(i)}) \right).\]

So the implementation will be easy if you understand the mathematical notation above.

def compute_loss(Y, Y_hat):
    """
    compute loss function
    """
    L_sum = np.sum(np.multiply(Y, np.log(Y_hat)))
    m = Y.shape[1]
    L = -(1./m) * L_sum

    return L

Train step

Notice that at this phase, we introduce three dictionaries: params, cache, and grads which corresponding hold the parameters of weights and biases, activations and gradients. These is pretty convenient for storing and accessing those parameters and make it easy to read.

Feed Forward

The forward pass on a single example $x$ executes the following computation on each layer of Neural Networks:

\[\hat{y} = \sigma(w^T x + b).\]

where $\sigma(z)$ is the sigmoid() we defined above.

Aside: In particular, rectiﬁed linear units (ReLU) have proven very successful for multi-layer neural networks. You would better use ReLU as the activation function of the hidden layers.

def feed_forward(X, params):
    """
    feed forward network: 2 - layer neural net

    inputs:
        params: dictionay a dictionary contains all the weights and biases

    return:
        cache: dictionay a dictionary contains all the fully connected units and activations
    """
    cache = {}

    # Z1 = W1.dot(x) + b1
    cache["Z1"] = np.matmul(params["W1"], X) + params["b1"]

    # A1 = sigmoid(Z1)
    cache["A1"] = sigmoid(cache["Z1"])

    # Z2 = W2.dot(A1) + b2
    cache["Z2"] = np.matmul(params["W2"], cache["A1"]) + params["b2"]

    # A2 = softmax(Z2)
    cache["A2"] = np.exp(cache["Z2"]) / np.sum(np.exp(cache["Z2"]), axis=0)

    return cache

Back Propagation

Aside: There is an amazing course offered by Stanford (Stanford CS231n) and this lecture is mainly talking about Back Propagation. If you prefer to video rather than dull mathematical formulas. Go for it!

For backpropagation, we’ll need to know how $L$ changes with respect to each component $w_j$ of $w$. That is, we must compute each $ \frac{\partial L}{\partial w_j} $.

In order to perform classification, a softmax layer is added to the neural network. The objective function is the negative log-likelihood (commonly also called the cross-entropy error):

\[\begin{align} z &= w^T x + b,\newline \hat{y} &= \sigma(z),\newline L(y, \hat{y}) &= -y \log(\hat{y}) - (1-y) \log(1-\hat{y}). \end{align}\]

And back propagation is actually a fancy name of chain rules. So if you are familiar with Calculus, you will see:

\[\frac{\partial L}{\partial w_j} = \frac{\partial L}{\partial \hat{y}} \frac{\partial \hat{y}}{\partial z} \frac{\partial z}{\partial w_j}.\]

Let us focusing on $ \frac{\partial L}{\partial \hat{y}} $ first:

\[\begin{align} \frac{\partial L}{\partial \hat{y}} &= \frac{\partial}{\partial \hat{y}} \left( -y \log(\hat{y}) - (1-y) \log(1-\hat{y}) \right)\newline &= -y \frac{\partial}{\partial \hat{y}} \log(\hat{y}) - (1-y) \frac{\partial}{\partial \hat{y}} \log(1-\hat{y})\newline &= \frac{-y}{\hat{y}} + \frac{(1-y) }{1 - \hat{y}}\newline &= \frac{\hat{y} - y}{\hat{y}(1 - \hat{y})}. \end{align}\]

Then followed by the chain rule, we can get:

\[\begin{align} \frac{\partial}{\partial z} \sigma(z) &= \frac{\partial}{\partial z} \left( \frac{1}{1 + e^{-z}} \right)\newline &= - \frac{1}{(1 + e^{-z})^2} \frac{\partial}{\partial z} \left( 1 + e^{-z} \right)\newline &= \frac{e^{-z}}{(1 + e^{-z})^2}\newline &= \frac{1}{1 + e^{-z}} \frac{e^{-z}}{1 + e^{-z}}\newline &= \sigma(z) \frac{e^{-z}}{1 + e^{-z}}\newline &= \sigma(z) \left( 1 - \frac{1}{1 + e^{-z}} \right)\newline &= \sigma(z) \left( 1 - \sigma(z) \right)\newline &= \hat{y} (1-\hat{y}). \end{align}\]

Collecting our results, the Stochastic Gradient Descent algorithm for updating $\theta$ is:

For more detailed calculation of Back Propagation, you can find my previous assignment solution related to Back Propagation of CS446: Machine Learning at UIUC here

def back_propagate(X, Y, params, cache, m_batch):
    """
    back propagation

    inputs:
        params: dictionay a dictionary contains all the weights and biases
        cache: dictionay a dictionary contains all the fully connected units and activations

    return:
        grads: dictionay a dictionary contains the gradients of corresponding weights and biases
    """
    # error at last layer
    dZ2 = cache["A2"] - Y

    # gradients at last layer (Py2 need 1. to transform to float)
    dW2 = (1. / m_batch) * np.matmul(dZ2, cache["A1"].T)
    db2 = (1. / m_batch) * np.sum(dZ2, axis=1, keepdims=True)

    # back propgate through first layer
    dA1 = np.matmul(params["W2"].T, dZ2)
    dZ1 = dA1 * sigmoid(cache["Z1"]) * (1 - sigmoid(cache["Z1"]))

    # gradients at first layer (Py2 need 1. to transform to float)
    dW1 = (1. / m_batch) * np.matmul(dZ1, X.T)
    db1 = (1. / m_batch) * np.sum(dZ1, axis=1, keepdims=True)

    grads = {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}

    return grads

Training

Hyper-parameters settings

These are the hyper-parameters which need to be tuned:

learning rate
training epochs
beta (SGD with momentum)
batch size

import argparse

parser = argparse.ArgumentParser()

# hyperparameters setting
parser.add_argument('--lr', type=float, default=0.5, help='learning rate')
parser.add_argument('--epochs', type=int, default=50,
                    help='number of epochs to train')
parser.add_argument('--n_x', type=int, default=784, help='number of inputs')
parser.add_argument('--n_h', type=int, default=64,
                    help='number of hidden units')
parser.add_argument('--beta', type=float, default=0.9,
                    help='parameter for momentum')
parser.add_argument('--batch_size', type=int,
                    default=64, help='input batch size')

# parse the arguments
opt = parser.parse_args()

Training process can be simplified as a loop forward pass -> compute loss -> back propagation -> update weights and bias -> forward pass

# training
for i in range(opt.epochs):

    # shuffle training set
    permutation = np.random.permutation(X_train.shape[1])
    X_train_shuffled = X_train[:, permutation]
    Y_train_shuffled = Y_train[:, permutation]

    for j in range(batches):

        # get mini-batch
        begin = j * opt.batch_size
        end = min(begin + opt.batch_size, X_train.shape[1] - 1)
        X = X_train_shuffled[:, begin:end]
        Y = Y_train_shuffled[:, begin:end]
        m_batch = end - begin

        # forward and backward
        cache = feed_forward(X, params)
        grads = back_propagate(X, Y, params, cache, m_batch)

        # with momentum (optional)
        dW1 = (opt.beta * dW1 + (1. - opt.beta) * grads["dW1"])
        db1 = (opt.beta * db1 + (1. - opt.beta) * grads["db1"])
        dW2 = (opt.beta * dW2 + (1. - opt.beta) * grads["dW2"])
        db2 = (opt.beta * db2 + (1. - opt.beta) * grads["db2"])

        # gradient descent
        params["W1"] = params["W1"] - opt.lr * dW1
        params["b1"] = params["b1"] - opt.lr * db1
        params["W2"] = params["W2"] - opt.lr * dW2
        params["b2"] = params["b2"] - opt.lr * db2

    # forward pass on training set
    cache = feed_forward(X_train, params)
    train_loss = compute_loss(Y_train, cache["A2"])

    # forward pass on test set
    cache = feed_forward(X_test, params)
    test_loss = compute_loss(Y_test, cache["A2"])
    print("Epoch {}: training loss = {}, test loss = {}".format(
        i + 1, train_loss, test_loss))

Results

After training for 50 epochs on the entire MNIST dataset, we reach $ 98\% $ precision, $ 98\% $ recall and $ 98\% $ f1-score!

             precision    recall  f1-score   support

          0       0.99      0.98      0.98       997
          1       0.99      0.99      0.99      1138
          2       0.98      0.98      0.98      1032
          3       0.98      0.97      0.97      1019
          4       0.98      0.98      0.98       984
          5       0.97      0.98      0.97       883
          6       0.98      0.98      0.98       953
          7       0.97      0.98      0.98      1017
          8       0.98      0.98      0.98       974
          9       0.96      0.97      0.97      1003

avg / total       0.98      0.98      0.98     10000