542. 01 Matrix

Problem Description

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

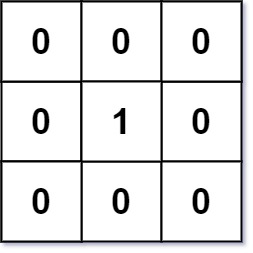
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

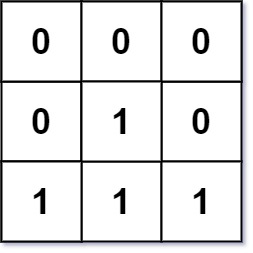
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 104
1 <= m * n <= 104
mat[i][j] is either 0 or 1.
There is at least one 0 in mat.

Solution

video

• BFS
• DP

Python

import sys

from collections import deque

class Solution:

    def __init__(self):
        self.dx = [1, -1, 0, 0]
        self.dy = [0, 0, 1, -1]
    
    def updateMatrix(self, matrix: List[List[int]]) -> List[List[int]]:

        if not matrix or len(matrix) == 0 or len(matrix[0]) == 0:
            return matrix

        n, m = len(matrix), len(matrix[0])
        dist = [[0 for _ in range(m)] for _ in range(n)]
        queue = deque([])

        for i in range(n):
            for j in range(m):
                if matrix[i][j] == 0:
                    dist[i][j] = 0
                    queue.append([i, j])
                else:
                    dist[i][j] = sys.maxsize
        
        while queue:
            x, y = queue.popleft()
            for d in range(4):
                next_x, next_y = x + self.dx[d], y + self.dy[d]
                if self.isValid(next_x, next_y, matrix):
                    if (dist[next_x][next_y] > dist[x][y] + 1):
                        dist[next_x][next_y] = dist[x][y] + 1
                        queue.append([next_x, next_y])

        return dist


    def isValid(self, x, y, matrix):
        return 0 <= x < len(matrix) and 0 <= y < len(matrix[0])

Java

class Solution {
    public int[][] updateMatrix(int[][] matrix) {
        if (matrix.length == 0 || matrix[0].length == 0) {
            return matrix;
        }
        int[][] dis = new int[matrix.length][matrix[0].length];
        int range = matrix.length * matrix[0].length;

        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == 0) {
                    dis[i][j] = 0;
                } else {
                    int upCell = (i > 0) ? dis[i - 1][j] : range;
                    int leftCell = (j > 0) ? dis[i][j - 1] : range;
                    dis[i][j] = Math.min(upCell, leftCell) + 1;
                }
            }
        }

        for (int i = matrix.length - 1; i >= 0; i--) {
            for (int j = matrix[0].length - 1; j >= 0; j--) {
                if (matrix[i][j] == 0) {
                    dis[i][j] = 0;
                } else {
                    int downCell = (i < matrix.length - 1) ? dis[i + 1][j] : range;
                    int rightCell = (j < matrix[0].length - 1) ? dis[i][j + 1] : range;
                    dis[i][j] = Math.min(Math.min(downCell, rightCell) + 1, dis[i][j]);
                }
            }
        }

        return dis;
    }
}

Complexity Analysis

• Time Complexity
  • O(NM)
• Space Complexity
  • O(NM)