799. Champagne Tower
Problem Description
We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row. Each glass holds one cup of champagne.
Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.

Now after pouring some non-negative integer cups of champagne, return how full the jth glass in the ith row is (both i and j are 0-indexed.)
Example 1:
Input: poured = 1, query_row = 1, query_glass = 1
Output: 0.00000
Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.
Example 2:
Input: poured = 2, query_row = 1, query_glass = 1
Output: 0.50000
Explanation: We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.
Example 3:
Input: poured = 100000009, query_row = 33, query_glass = 17
Output: 1.00000
Constraints:
0 <= poured <= 109
0 <= query_glass <= query_row < 100
Solution
This question is pretty similar to 118. Pascal’s Triangle
You can simplify the original problem as follows, where the remainder of c[i][j] will be “sent” to c[i + 1][j] and c[i + 1][j + 1] equally. So we can get the top-to-down dynamic programming solution easily
c c
c c c c
c c c => c c c
c c c c c c c c
c c c c c c c c c c
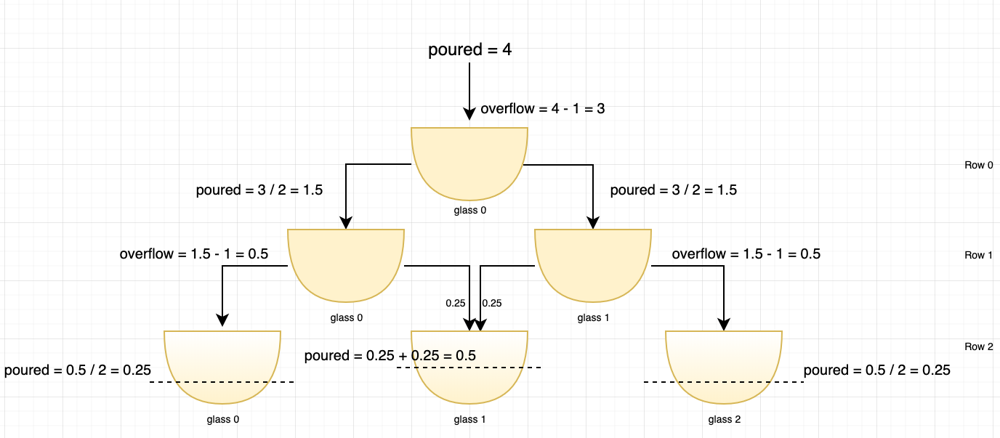
Source: Discussion post in Leetcode
Top-to-down Dynamic Programming
class Solution:
def champagneTower(self, poured: int, n: int, m: int) -> float:
for i in range(query_row):
for j in range(0, i + 1):
flow = (dp[i][j] - 1) / 2
if flow > 0:
dp[i + 1][j] += flow
dp[i + 1][j + 1] += flow
return min(1,dp[query_row][query_glass])
Down-to-top Dynamic Programming
You can also write a down-to-top version but this is not as easy to understand as the above solution
class Solution:
def champagneTower(self, poured: int, n: int, m: int) -> float:
f = [[0 for _ in range(n + 2)] for _ in range(1, n + 2)]
delta = [[0 for _ in range(n + 2)] for x in range(1, n + 2)]
f[0][0] = 1 if poured >= 1 else poured
delta[0][0] = (poured - f[0][0]) / 2
for i in range(1, n + 1):
for j in range(i + 1):
if j == 0:
f[i][j] = 1 if delta[i - 1][j] >= 1 else delta[i - 1][j]
delta[i][j] = (delta[i - 1][j] - f[i][j]) / 2
else:
f[i][j] = 1 if delta[i - 1][j] + delta[i - 1][j - 1] >= 1 else delta[i - 1][j] + delta[i - 1][j - 1]
delta[i][j] = (delta[i - 1][j] + delta[i - 1][j - 1] - f[i][j]) / 2
return f[n][m] if f[n][m] <= 1 else 1
Complexity Analysis
- Time Complexity
- O(n^2), where n is number of rows and
- Space Complexity
- O(n) - this can be optimized to O(1) using rolling array