235. Lowest Common Ancestor of a Binary Search Tree

Problem Description

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

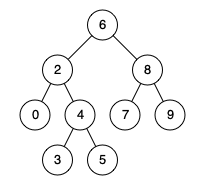
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

Constraints:

The number of nodes in the tree is in the range [2, 105].
-10^9 <= Node.val <= 10^9
All Node.val are unique.
p != q
p and q will exist in the BST.

Solution

Using attribute of Binary Search Tree to do Divide and Conquer

Python

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root or not p or not q:
            return None

        return self._findLCA(root, p, q)


    def _findLCA(self, root, p, q):
        if root == p or root == q:
            return root

        if root.val < p.val and root.val < q.val:
            return self._findLCA(root.right, p, q)
        elif root.val > p.val and root.val > q.val:
            return self._findLCA(root.left, p, q)
        else:
            return root

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || p == null || q == null) {
            return null;
        }

        return findLCA(root, p, q);
    }


    private TreeNode findLCA(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return root;
        }

        if (root == p || root == q) {
            return root;
        }

        if (root.val < p.val && root.val < q.val) {
            return findLCA(root.right, p, q);
        } else if (root.val > p.val && root.val > q.val) {
            return findLCA(root.left, p, q);
        }   else {
            return root;
        }

    }

}

Complexity Analysis

• Time Complexity
  • O(H), where H is the height of Binary Search Tree
    • Worst case: O(n)
    • Average case: O(logn)
• Space Complexity
  • O(1)