236. Lowest Common Ancestor of a Binary Tree
Problem Description
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
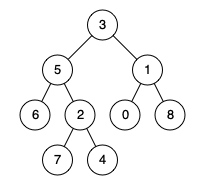
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [1,2], p = 1, q = 2
Output: 1
Constraints:
- The number of nodes in the tree is in the range [2, 105].
- -109 <= Node.val <= 109
- All Node.val are unique.
- p != q
- p and q will exist in the tree.
Solution
This is a Binary Tree related problem. When it comes to binary tree, finding some nodes or some paths that meet the requirements, the first algorithm is “Divide and Conquer”. I just mark this question as a DFS problem for simplification, but if you have worked on several problems, I personally think D&C is a special case of DFS (since there are two branches in D&C, but in DFS there can be multiple)
Now, we have already confirm the algorithm we are going to use, let’s check this problem for more details.
By checking the examples, there are three different cases in finding the LCA
Example: finding the LCA of 4 and 5
case 1: 4 and 5 are on the left and right subtree, not in the same subtree
3
/ \
4 5
case 2 and 3: 4 and 5 are on the same side
3 3
\ /
5 4
\ /
4 5
- for case 1: we will return the root of 4 and 5
- for case 2: we can return either 4 or 5 but that node should be the ancestor of the other
Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
return self._find(root, p, q)
def _find(self, root, p, q):
if root is None or root == p or root == q:
return root
left_node = self._find(root.left, p, q)
right_node = self._find(root.right, p, q)
if right_node and not left_node:
return right_node
if left_node and not right_node:
return left_node
if left_node and right_node:
return root
return None
Java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
return findLCA(root, p, q);
}
private TreeNode findLCA(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q)
return root;
TreeNode left = findLCA(root.left, p, q);
TreeNode right = findLCA(root.right, p, q);
if (left == null && right == null)
// did not find the LCA
return null;
else if (left == null && right != null)
// LCA is not found in left subtree but in right subtree
return right;
else if (left != null && right == null)
// same logic as above
return left;
else if (left != null && right != null)
// LCA is found in both subtree, why?
// this is the logic for example 1
// the "LCA" founded in both subtree is actually the node of `p` and `q`
// which means the LCA is the root/parent node of the both
return root;
return null;
}
}