566. Reshape the Matrix

Problem Description

In MATLAB, there is a handy function called reshape which can reshape an m x n matrix into a new one with a different size r x c keeping its original data.

You are given an m x n matrix mat and two integers r and c representing the row number and column number of the wanted reshaped matrix.

The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.

If the reshape operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.

Example 1:

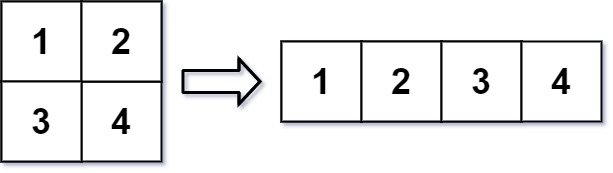
Input: mat = [[1,2],[3,4]], r = 1, c = 4
Output: [[1,2,3,4]]

Example 2:

Input: mat = [[1,2],[3,4]], r = 2, c = 4
Output: [[1,2],[3,4]]

Constraints:

- m == mat.length
- n == mat[i].length
- 1 <= m, n <= 100
- -1000 <= mat[i][j] <= 1000
- 1 <= r, c <= 300

Solution

Python

class Solution:
    def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:
        if not mat or len(mat) == 0 or len(mat[0]) == 0:
            return mat

        n, m = len(mat), len(mat[0])
        if n * m != r * c:
            return mat

        # reshap matrix
        ret = [[0 for _ in range(c)] for _ in range(r)]
        for i in range(n):
            for j in range(m):
                xy = i * m + j
                new_x = xy // c
                new_y = xy % c
                ret[new_x][new_y] = mat[i][j]

        return ret

Java

class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        if (mat == null || mat.length == 0 || mat[0].length == 0)
            return mat;

        int n = mat.length, m = mat[0].length;
        if (n * m != r * c)
            return mat;

        int[][] ret = new int[r][c];

        for (int i = 0; i < n; i++) {
            for ( int j = 0; j < m; j++) {
                int xy = i * m + j;
                int x = xy / c;
                int y = xy % c;
                ret[x][y] = mat[i][j];
            }
        }

        return ret;
    }
}

Complexity Analysis

• Time Complexity
  • O(n*m) Traverse mat array
• Space Complexity
  • O(1)